2023年七上數學：有理數章節考點大匯總

有理數的概念

一、本節學習指導本節知識點比較多，同學們要認真學習并加以總結，用自己的語言來理解部分知識是有助于我們記憶的。對于本節的知識如果一時記不住也不要急，畢竟我們才剛剛進入初級數學的學習。

二、知識要點1、正數和負數(1)、大于0的數叫做正數。(2)、在正數前面加上負號“-”的數叫做負數。(3)、數0既不是正數，也不是負數，0是正數與負數的分界。(4)、在同一個問題中，分別用正數與負數表示的量具有相反的意義。

2、有理數(1)凡能寫成分數形式的數，都是有理數，整數和分數統稱有理數.注意：0即不是正數，也不是負數;-a不一定是負數，如：-(-2)=4，這個時候的a=-2。p不是有理數;(2)有理數的分類:

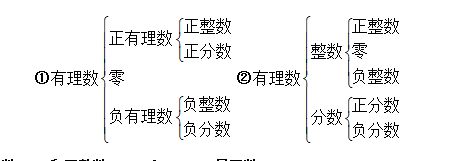
(3)

3、數軸【重點】

(1)、用一條直線上的點表示數，這條直線叫做數軸。它滿足以下要求：① 在直線上任取一個點表示數0，這個點叫做原點;② 通常規定直線上從原點向右(或上)為正方向，從原點向左(或下)為負方向;③選取適當的長度為單位長度，直線上從原點向右，每隔一個單位長度取一個點，依次表示1,2,3…;從原點向左，用類似的方法依次表示-1,-2，-3…(2)、數軸的三要素：原點、正方向、單位長度。(3)、畫數軸的步驟：一畫(畫一條直線并選取原點);二取(取正反向);三選(選取單位長度);四標(標數字)。數軸的規范畫法：是條直線，數字在下，字母在上。注意：所有的有理數都可以用數字上的點表示，但是數軸上的所有點并不都表示有理數。(4)、一般地，設a是一個正數，則數軸上表示數a的點在原點的右邊，與原點的距離是a個單位長度;表示數-a的點在原點的左邊，與原點的距離是a個單位長度。

4、相反數

(1)、只有符號不同的兩個數叫做互為相反數。① 注意：a的相反數是-a;a-b的相反數是b-a;a+b的相反數是-(a+b)=-a-b;② 非零數的相反數的商為-1; ③ 相反數的絕對值相等。(2)、一般地，設a是一個正數，數軸上與原點的距離是a的點有兩個，他們分別在原點的兩側，表示a和-a，我們說這兩點關于原點對稱。(3)、a和-a互為相反數。0的相反數是0，正數的相反數是負數，負數的相反數是正數。相反數是它本身的數只有0。(4)、在任意一個數前面添上“-”號，新的數就表示原數的相反數。(5)、若兩個數a、b互為相反數，就可以得到a+b=0;反過來若a+b=0，則a、b互為相反數。(6)、多重符號的相乘由“-”的個數來定：若“-”的個數為偶數，相乘結果為正數;若“-“的個數為奇數，化簡結果為負數。比如：-2×4×(-3)×(-1)×(-5)，首先由4個負號，所以最終結果是正數，再算數字相乘得到120

5、絕對值(1)、絕對值的定義：一個數a的絕對值就是數軸上表示數a的點與原點的距離。數a的絕對值記作|a|。(2)、正數的絕對值等于它本身;0的絕對值是0(或者說0的絕對值是它本身，或者說0的絕對值是它的相反數);負數的絕對值等于它的相反數;(注意：絕對值的意義是數軸上表示某數的點離開原點的距離;)。0是絕對值最小的數。

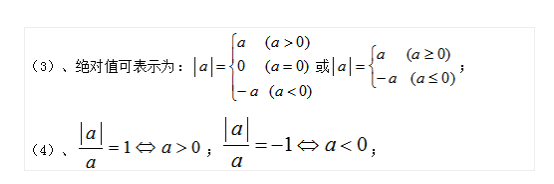
(5)、任何數的絕對值總是非負數(非負數是正數或0)，即|a|≥0。(6)、互為相反數的兩個數的絕對值相等。絕對值相等的兩個數可能是互為相反數或者相等。(7)、有理數比大小：① 正數比0大，0大于負數，正數大于負數;② 兩個負數比較，絕對值大的反而小;③ 數軸上的兩個數，右邊的數總比左邊的數大;(8)、比較兩個負數的大小的步驟如下：①先求出兩個數負數的絕對值;②比較兩個絕對值的大小;③根據“兩個負數，絕對值大的反而小”做出正確的判斷。三、經驗之談：本節我們要理解很多的名詞概念，希望同學們多讀幾遍。其次我們還要重點理解正數和負數的關系，以及對絕對值幾何意義，還有數軸的畫法。總之本節我們要認真學習。

有理數的運算

一、本節學習指導有理數的運算和我們小學學習的四則運算很相似，運算規律都一樣，不同的是有負數參與，所以相對要復雜一些，本節要多加練習。本節有配套學習視頻。二、知識要點1、有理數的加法(1)、有理數加法法則：① 同號兩數相加，取相同的符號，并把絕對值相加;② 異號兩數相加，取絕對值較大加數的符號，并用較大的絕對值減去較小的絕對值;③ 一個數與0相加，仍得這個數.(2)、加法計算步驟：先定符號，再算絕對值。(3)、有理數加法的運算律：① 加法的交換律：a+b=b+a;② 加法的結合律：(a+b)+c=a+(b+c).(4)、為了計算簡便 ，往往會采取以下方法：①互為相反的兩個數，可以先相加;②符號相同的數，可以先相加;③分母相同的數，可以先相加;④幾個數相加能得到整數，可以先相加。2、有理數的減法(1)、有理數減法法則：減去一個數，等于加上這個數的相反數;即a-b=a+(-b).(有理數減法運算時注意兩“變”：①減法變加法;②把減數變為它的相反數.)注：有理數的減法實質就是把減法變加法。3、有理數的乘法(1)、有理數乘法法則：①兩數相乘，同號得正，異號得負，并把絕對值相乘;②任何數同零相乘都得零;(2)、一個數同1相乘，結果是原數;一個數同-1相乘，結果是原數的相反數。(3)、乘積為1的兩個數互為倒數;注意：0沒有倒數;若ab=1<====>a、b互為倒數。(4)、幾個不是偶的數相乘，積的符號由負因式的個數決定。負因數的個數是偶數時，積是正數;負因數的個數是奇數是，積是負數。(5)、有理數乘法的運算律：① 乘法的交換律：ab=ba;② 乘法的結合律：(ab)c=a(bc);③ 乘法的分配律：a(b+c)=ab+ac.4、有理數的除法(1)、有理數除法法則：除以一個不等于0的數，等于乘這個數的倒數。(2)、有理數除法符號法則：兩數相除，同號得正，異號得負，并把絕對值相除。0除以任何一個不等于0的數，都得0。(3)、乘除混合運算的步驟：①先把除法轉化為乘法;②確定積的符號;③運用乘法運算律和乘法法則進行計算得出結果。5、有理數的乘方(1)、求n個相同因數的積的運算，叫做乘方，乘方的結果叫做冪。在an中，a叫做底數，n叫做指數。(2)、an表示的意義是n個a相乘。如：2³=2×2×2=8(3)、分數的乘方，在書寫時一定要把整個分數用小括號括起來。如：(1/2)²(4)、負數的乘方，在書寫時一定要把整個負數(連同負號)用小括號括起來。(5)、10的幾次方，冪的結果中1后面就有幾個0。如：105=100000(6)、負數的奇次冪是負數，負數的偶次冪是正數。顯然，正數的任何次冪都是正數，0的任何正整數次冪都是0。1的任何次冪都是1。-1的奇數次冪是-1，-1的偶數次冪是1。

6、科學記數法(1)、把一個大于10數表示成a×10n的形式(其中a是整數數位只有一位的數，而且1≤︱a︱<10，n是正整數)，使用的是科學計數法。(2)、用科學記數法表示一個n位整數，其中10的指數是n-1。例：240 000 000用科學計數法記為2.4×108

7、近似數(1)、接近實際數字，但是與實際數字還是有差別，這個數是一個近似數。(2)、精確度：近似數與準確數的接近程度可以用精確度表示。(3)、利用四舍五入法得到的近似數，四舍五入到哪一位，就說這個近似數精確到哪一位。(4)、從一個數的左邊的第一個非0數字起，到末尾數字止，所有的數字都是這個數的有效數字。(5)、解題技巧：①近似數精確到哪一位，只需看這個數的最末一位在原數的哪一位。②當四舍五入到十位或十位以上時，應先用科學記數法表示這個數，再按要求取近似數。(6)、a×10n中有效數字是指a的有效數字。7、等于本身的數匯總：① 相反數等于本身的數：0 ② 倒數等于本身的數：1，-1③ 絕對值等于本身的數：正數和0④ 平方等于本身的數：0,1

⑤ 立方等于本身的數：0,1，-1.

       編輯推薦：

       2023年中考各科目重點知識匯總

　　 歡迎使用手機、平板等移動設備訪問中考網，2025中考一路陪伴同行！>>點擊查看