來源:網(wǎng)絡(luò)資源 2022-11-21 18:50:19
初中代數(shù)相對于小學(xué)來說擴(kuò)大了數(shù)的范圍,從正整數(shù),正分?jǐn)?shù),零擴(kuò)大到對實數(shù)的研究,也引入了函數(shù)與低次方程不等式等相關(guān)內(nèi)容。
一.一元二次方程求兩根關(guān)系變形
①
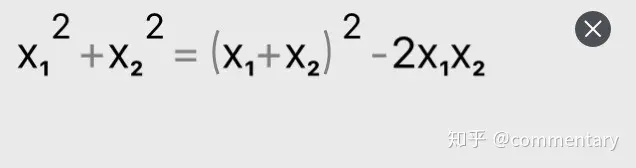
②
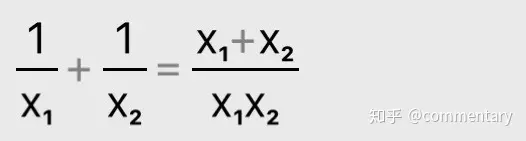
③
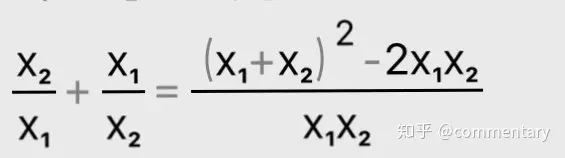
④
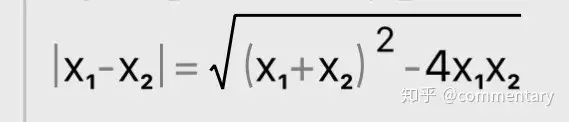
⑤
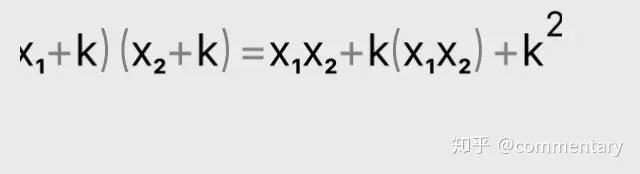
最左邊是x1
這里強(qiáng)烈推薦photomath,可以進(jìn)行數(shù)學(xué)運(yùn)算也可繪出函數(shù)圖像。
二.不等式
不等式符號若相同兩式可加減。
如:a+b>c 且e+f>d
則a+b+e+f>c+d
二次單項不等式可轉(zhuǎn)化成二次函數(shù)進(jìn)行求解。
如x²-2-8<0
①確定函數(shù)圖像
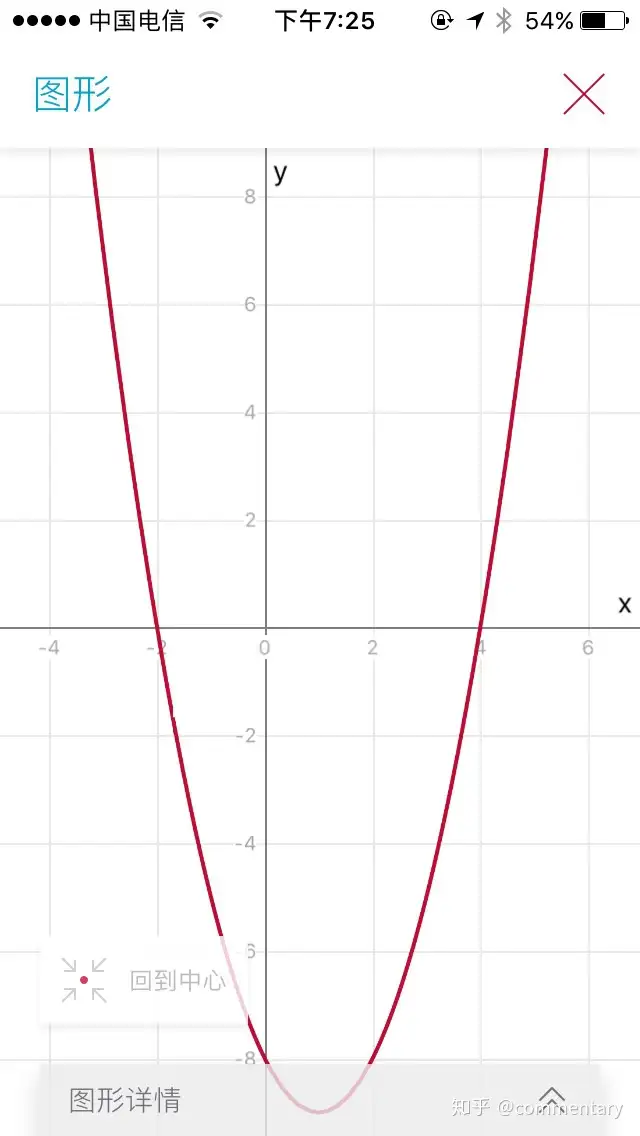
用的是上面的那個APP
②通過函數(shù)圖像可知函數(shù)圖像開口向上當(dāng)x的值為-2與4時函數(shù)值為0則當(dāng)函數(shù)值小于0x的取值范圍為-2<<4
若有絕對值的不等式則要分類討論。
如│x+5│+│x-7│<0
①確定當(dāng)x=-5,x=7為三區(qū)域的分界點(diǎn)
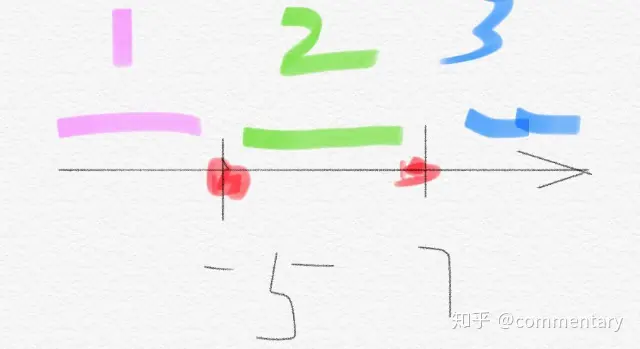
①當(dāng)x<-5時│x+5│<0且│x-7│<0去絕對值后進(jìn)行計算
②當(dāng)-50而│x-7│<0去絕對值后進(jìn)行計算
③當(dāng)x>7時│x+5│>0且│x-7│>0去絕對值后進(jìn)行計算
綜上所述通過計算無解
分式不等式可將分子與分母相乘于是轉(zhuǎn)化為函數(shù)進(jìn)行求解同上。相乘后其實只要確定開口畫出簡略函數(shù)圖像使分子分母分別等于0即為函數(shù)圖像與x軸的交點(diǎn)就可以確定不等式取值范圍(若分式后加了一個整式則將它轉(zhuǎn)化為一個分式)。
★蛇形穿根法解不等式
◎適用于幾個因式相乘的不等式。畫出數(shù)軸,取每個因式等于0時未知數(shù)的值標(biāo)在數(shù)軸上若開口向上從上穿,開口向下從下穿。因式次數(shù)為奇穿為偶不穿(奇穿偶不穿)

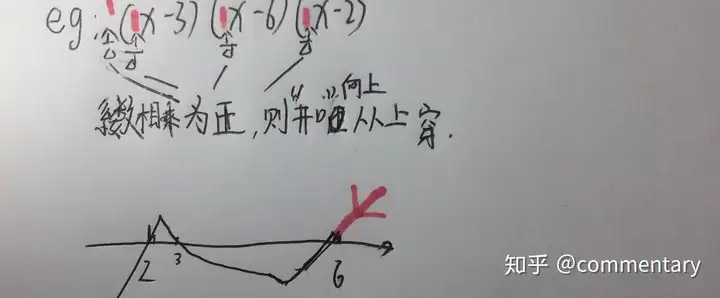
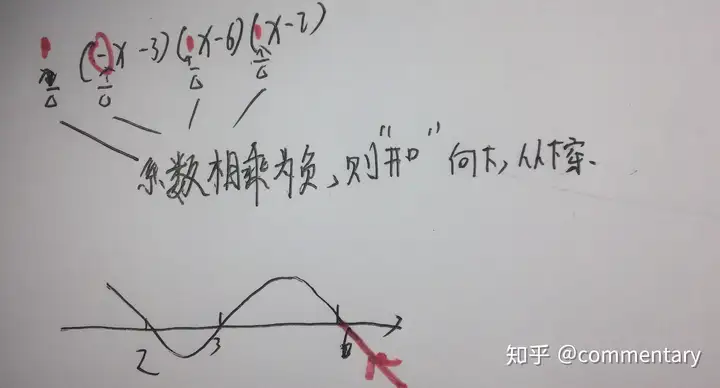

再通過圖像判斷取值范圍
(ps:因式內(nèi)降冪排列)
三.公式
①中點(diǎn)坐標(biāo)公式:已知點(diǎn)(x1,y1),(x2,y2)則有兩點(diǎn)所連直線中點(diǎn)坐標(biāo)為
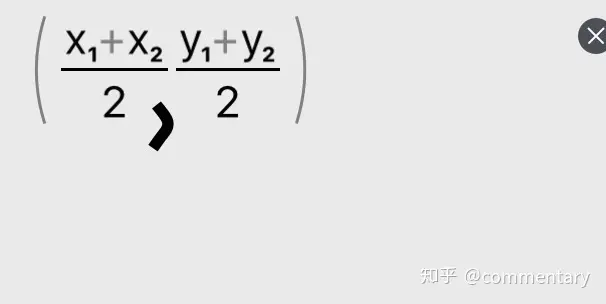
②求已知點(diǎn)(x,y)關(guān)于對稱軸直線x=a的對應(yīng)點(diǎn)為(2a-x,y)
③平面上n條直線最多有1/2(n-1)個交點(diǎn)
④基本比例式
若:

則ac=bd
⑤合分比
若:
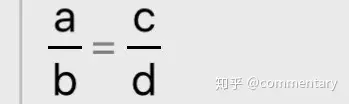
則:
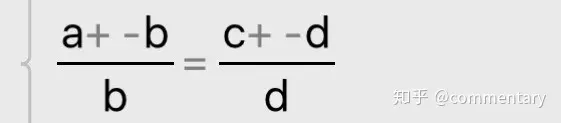
⑥等比:
若:
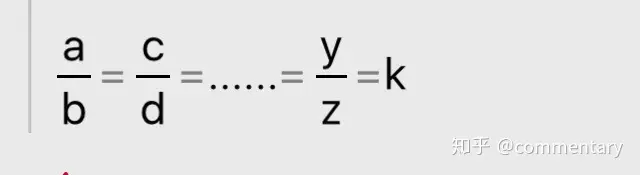
則:
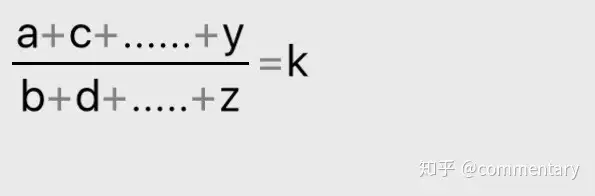
四.均值不等式(常用于物理功率最值問題):
若a、b均是正實數(shù),則:a+b≥2√(ab),當(dāng)且僅當(dāng)a=b時取等號.
(一正二定三相等)
歡迎使用手機(jī)、平板等移動設(shè)備訪問中考網(wǎng),2025中考一路陪伴同行!>>點(diǎn)擊查看